Organizing Containers of Balls

David has several containers, each with a number of balls in it. He has just enough containers to sort each type of ball he has into its own container. David wants to sort the balls using his sort method.

As an example, David has n = 2 containers and 2 different types of balls, both of which are numbered from 0 to n - 1 = 1. The distribution of ball types per container are described by n x n an matrix of integers, M[container][type]. For example, consider the following diagram for M = [[1, 4], [2, 3]]:

In a single operation, David can swap two balls located in different containers.

The diagram below depicts a single swap operation:

David wants to perform some number of swap operations such that:

• Each container contains only balls of the same type.
• No two balls of the same type are located in different containers.

You must perform q queries where each query is in the form of a matrix, M. For each query, print Possible on a new line if David can satisfy the conditions above for the given matrix. Otherwise, print Impossible.

Function Description

Complete the organizingContainers function in the editor below. It should return a string, either Possible or Impossible.

organizingContainers has the following parameter(s):

• containter: a two dimensional array of integers that represent the number of balls of each color in each container

Input Format

The first line contains an integer q, the number of queries.

Each of the next q sets of lines is as follows:

1. The first line contains an integer n, the number of containers (rows) and ball types (columns).
2. Each of the next n lines contains n space-separated integers describing row M[i].

Constraints

• 1 <= q <= 10
• 1 <= n <= 100
• 0 <= M[container][type] <= 10⁹

Scoring

• For 33% of score, 1 <= n <= 1.
• For 100% of score, 1 <= n <= 100.

Output Format

For each query, print Possible on a new line if David can satisfy the conditions above for the given matrix. Otherwise, print Impossible.

Sample Input 0

1
2
3
4
5
6
7

2
2
1 1
1 1
2
0 2
1 1

Sample Output 0

1
2

Possible
Impossible

Explanation 0

We perform the following q = 2 queries:

1. The diagram below depicts one possible way to satisfy David’s requirements for the first query:

Thus, we print Possible on a new line.

2. The diagram below depicts the matrix for the second query:

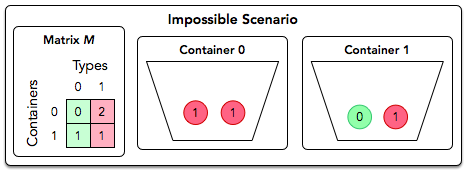
No matter how many times we swap balls of type t₀ and t₁ and between the two containers, we’ll never end up with one container only containing type t₀ and the other container only containing type t₁. Thus, we print Impossible on a new line.

Sample Input 1

1
2
3
4
5
6
7
8
9

2
3
1 3 1
2 1 2
3 3 3
3
0 2 1
1 1 1
2 0 0

Sample Output 1

1
2

Impossible
Possible

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

// Complete the organizingContainers function below.
function organizingContainers(container) {
  let result = true;

  let { row, col } = container.reduce(
    (target, items, index) => {
      items.reduce((itemTarget, item, subIndex) => {
        target["row"][index] += item;
        target["col"][subIndex] += item;

        return itemTarget;
      }, []);

      return target;
    },
    {
      row: new Array(container.length).fill(0),
      col: new Array(container.length).fill(0)
    }
  );

  row.sort();
  col.sort();

  for (let value of Array.from(
    { length: container.length },
    (value, index) => index
  )) {
    if (row[value] !== col[value]) {
      result = false;
      break;
    }
  }

  return result ? "Possible" : "Impossible";
}