Absolute Permutation

We define P to be a permutation of the first n natural numbers in the range [1, n]. Let pos[i] denote the value at position i in permutation P using 1-based indexing.

P is considered to be an absolute permutation if |pos[i] - i| = k holds true for every .

Given n and k, print the lexicographically smallest absolute permutation P. If no absolute permutation exists, print -1.

Example

n = 4

k = 2

Create an array of elements from 1 to n, pos = [1, 2, 3, 4]. Using based indexing, create a permutation where every |pos[i] - i| = k. It can be rearranged to [3, 4, 1, 2] so that all of the absolute differences equal k = 2:

1
2
3
4
5

pos[i]  i   |pos[i] - i|
  3     1        2
  4     2        2
  1     3        2
  2     4        2

Function Description

Complete the absolutePermutation function in the editor below.

absolutePermutation has the following parameter(s):

• int n: the upper bound of natural numbers to consider, inclusive
• int k: the absolute difference between each element’s value and its index

Returns

• int[n]: the lexicographically smallest permutation, or [-1] if there is none

Input Format

The first line contains an integer t, the number of queries.
Each of the next t lines contains 2 space-separated integers, n and k.

Constraints

• 1 <= t <= 10
• 1 <= n <= 10⁵
• 1 <= k < k

Sample Input

1
2
3
4
5
6

STDIN   Function
-----   --------
3       t = 3 (number of queries)
2 1     n = 2, k = 1
3 0     n = 3, k = 0
3 2     n = 3, k = 2

Sample Output

1
2
3

2 1
1 2 3
-1

Explanation

Test Case 0:

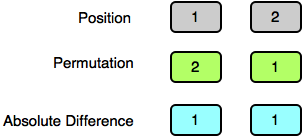
Test Case 1:

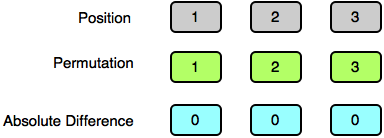
Test Case 2:

No absolute permutation exists, so we print -1 on a new line.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

/*
 * Complete the 'absolutePermutation' function below.
 *
 * The function is expected to return an INTEGER_ARRAY.
 * The function accepts following parameters:
 *  1. INTEGER n
 *  2. INTEGER k
 */

function absolutePermutation(n, k) {
  // Write your code here
  let result = [],
    contain = {},
    x,
    y;

  for (let i = 1; i <= n; i++) {
    x = i - k;
    y = i + k;

    switch (true) {
      case x > 0 && x <= n && !contain[x]:
        result.push(x);
        contain[x] = x;
        break;

      case y > 0 && y <= n && !contain[y]:
        result.push(y);
        contain[y] = y;
        break;

      default:
        return [-1];
    }
  }

  return result;
}